Projects
Overview
My research agenda focuses on developing machine learning approaches that efficiently utilize the abundance of energy data, accurately interpret physical energy system behaviors, provide cost-efficient and resilient solutions for emerging energy system challenges, and support the analysis of the societal impacts from the energy transition and climate change. I aim to identify key energy system applications that can be enabled or improved by new machine learning techniques, formulate energy system problems that highlight critical technical challenges, design efficient algorithms grounded in rigorous mathematical principles, and validate these methods using real-world testbeds or datasets.
In response to the rising need for intelligent solutions, harnessing the power of data is essential. The widespread deployment of smart meters in energy systems exemplifies this potential. However, current energy analytics tools face bottlenecks in high-fidelity data processing, particularly because energy data is often partially observable. For example, Behind-the-Meter (BTM) solar systems result in grid operators observing only aggregated measurements of load and solar generation. Synchrophasor data in power transmission systems suffers from missing/corrupted values, leaving system dynamics unobservable. These challenges raise the following research questions in energy systems:
Q1: How can we effectively extract information for decision-making, when facing large-scale, partially observable energy data?
Meeting the critical demands of information extraction for energy systems often requires more than simply scaling up existing machine learning methods. It is essential to leverage the inherent structure of energy data to extract information effectively. Moreover, common challenges with large-scale energy data lie not only in the complexity of the processes that generate it but also in the downstream decision-making processes it aims to inform and optimize. For example, electricity price formation relies on power flow models that incorporate congestion and account for the uncertainty introduced by renewable generation variability. Strategic energy storage must consider future price uncertainty while modeling physical constraints. Understanding and modeling energy system decision processes under uncertainty is critical for accurately learning from observed behaviors. This highlights another research question in designing energy systems:
Q2: How can we build an autonomous energy system that learns from complex, structured data, while improving decision quality under uncertainty?
My overarching research seeks to address the above questions by developing intelligent, cost-efficient, and resilient solutions that bridge machine learning with the evolving needs of energy systems
![]()
Learning-Enabled Autonomous Energy Storage Systems
The central theme of my postdoctoral research is enhancing decision-making for energy systems under uncertainty. Energy storage systems must strategically plan their operations based on future price forecasts to quantify their opportunity value, considering their limited energy capacity. These systems integrate various modules—electricity price prediction, market participation, cybersecurity, and risk-averse operation—into a cohesive framework for optimal decision-making. My research spans these critical components to advance the capabilities of autonomous energy storage operations.
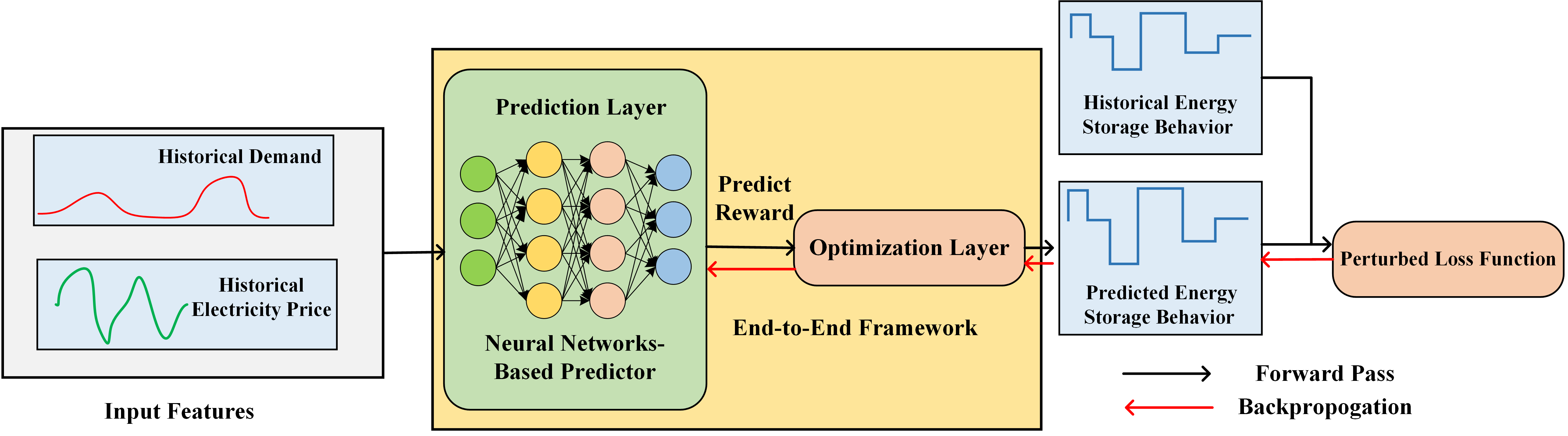
Strategic Energy Storage: Bridging Prediction and Optimization with Decision-Focused Learning. Energy storage systems typically employ Model Predictive Control (MPC) policy, which decouples price prediction from storage optimization. However, this separation introduces challenges, as machine learning models often fail to account for how predictions interact with energy storage optimization. I developed an end-to-end model that integrates price prediction and optimization, ensuring the training objective is directly aligned with final storage decisions. To ensure differentiability in linear storage models, the perturbation idea was introduced into the decision-focused loss function and provided a rigorous theoretical analysis of the perturbed loss. Our surrogate loss function bypasses expensive Jacobian computations, providing a more efficient model training. This method effectively addresses challenges in self-scheduling storage arbitrage, and storage behavior forecasting.
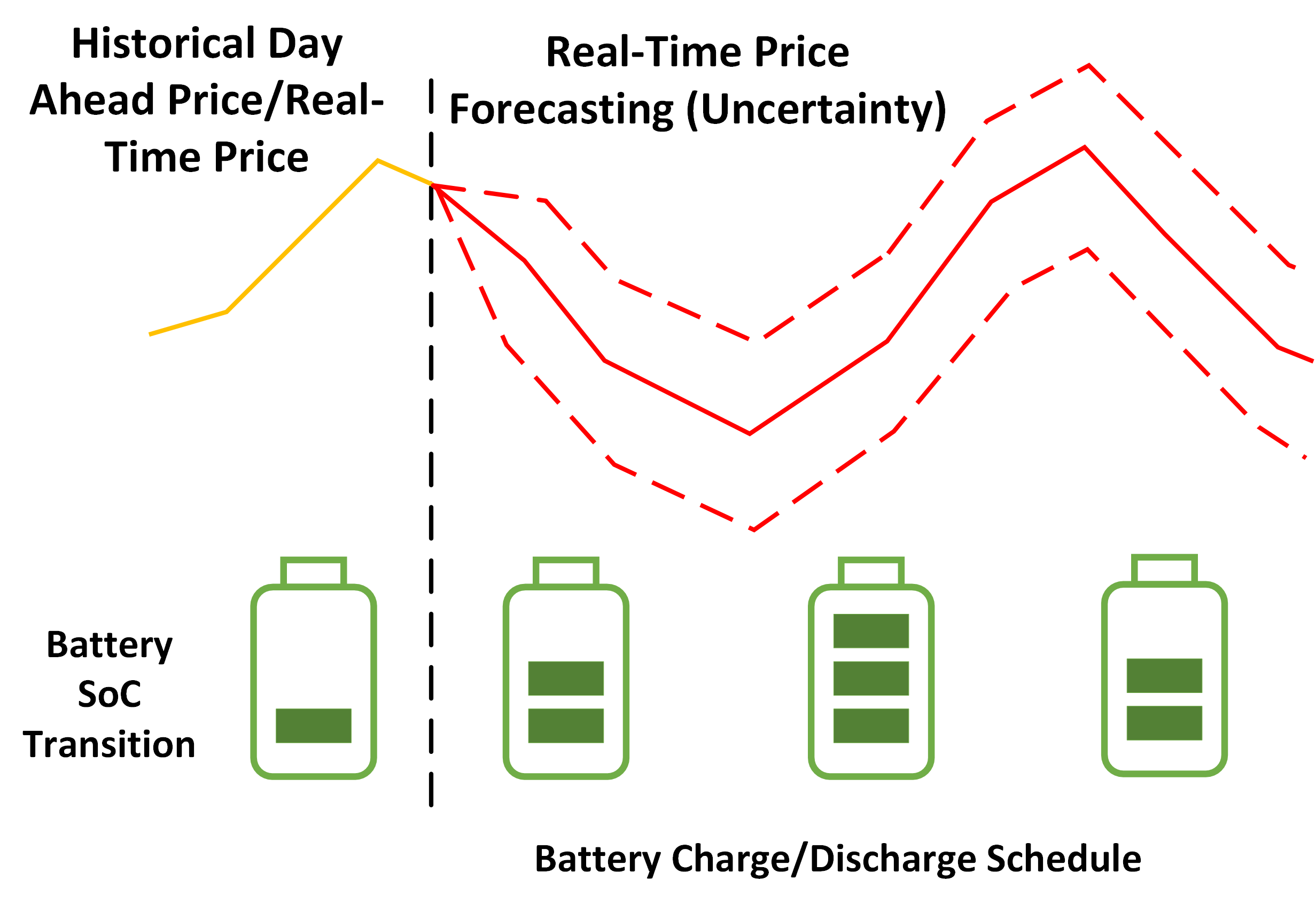
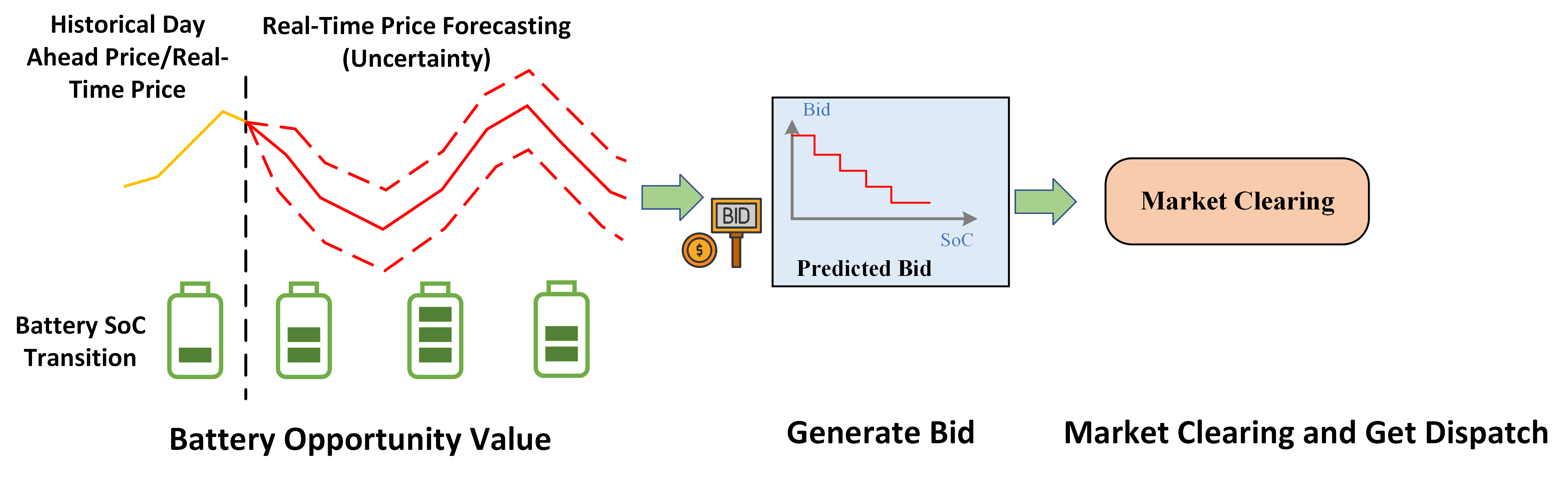
Decision-Focused Learning for Energy Storage Bidding.
I extended the decision-focused framework to tackle storage bidding, a more complex challenge where storage systems must place bids in advance rather than making real-time charge/discharge decisions. Along with degradation costs, the bidding model must account for opportunity costs that result from limited storage capacity. Given future price forecasting, the key idea for bidding design is to link the opportunity cost to the dual variable of the state of charge (SoC). Training an end-to-end bidding framework with a decision-focused loss is challenging due to the dual optimization layers for bid generation and market clearing. Leveraging the implicit function theorem, the decision loss is backpropagated through dual differentiable optimization layers to update the predictor’s weights. This approach yields higher profits and generalizes well to price-maker scenarios, providing a versatile solution for real-world applications.
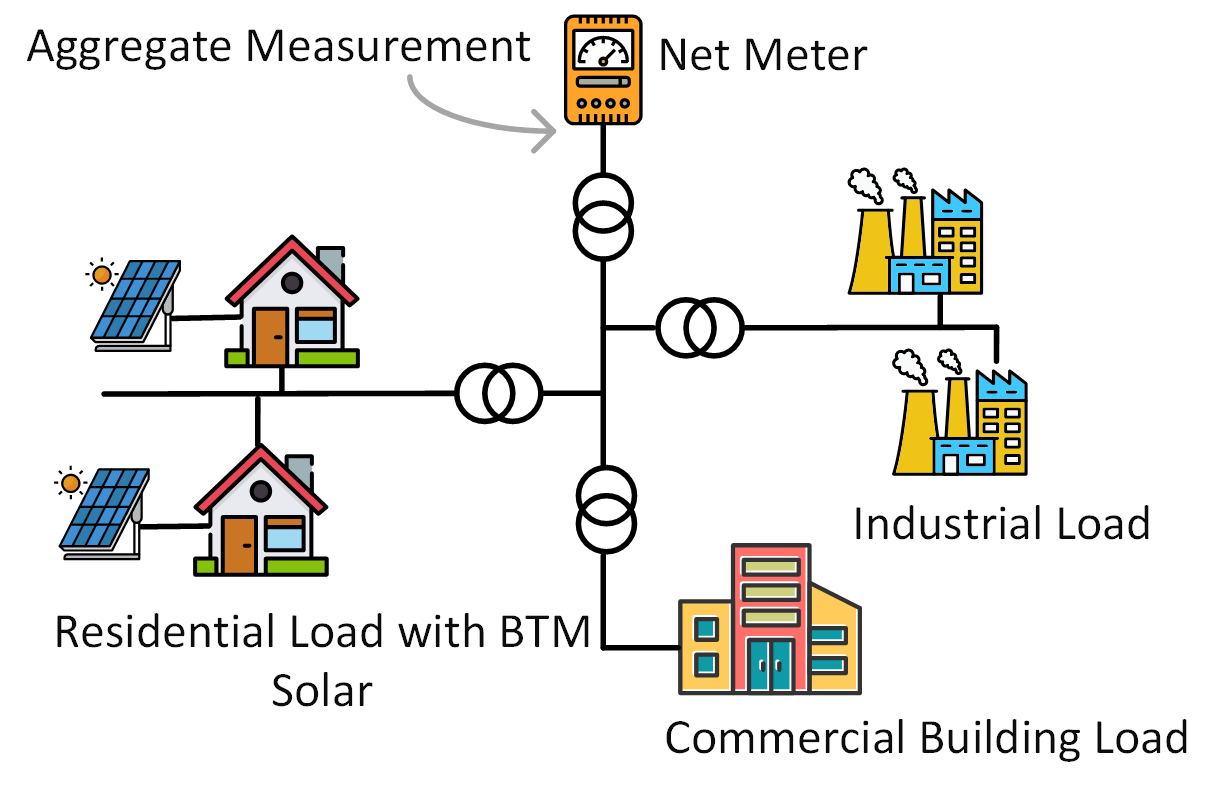
Energy Disaggregation at Substations with Behind-the-Meter Solar Generation
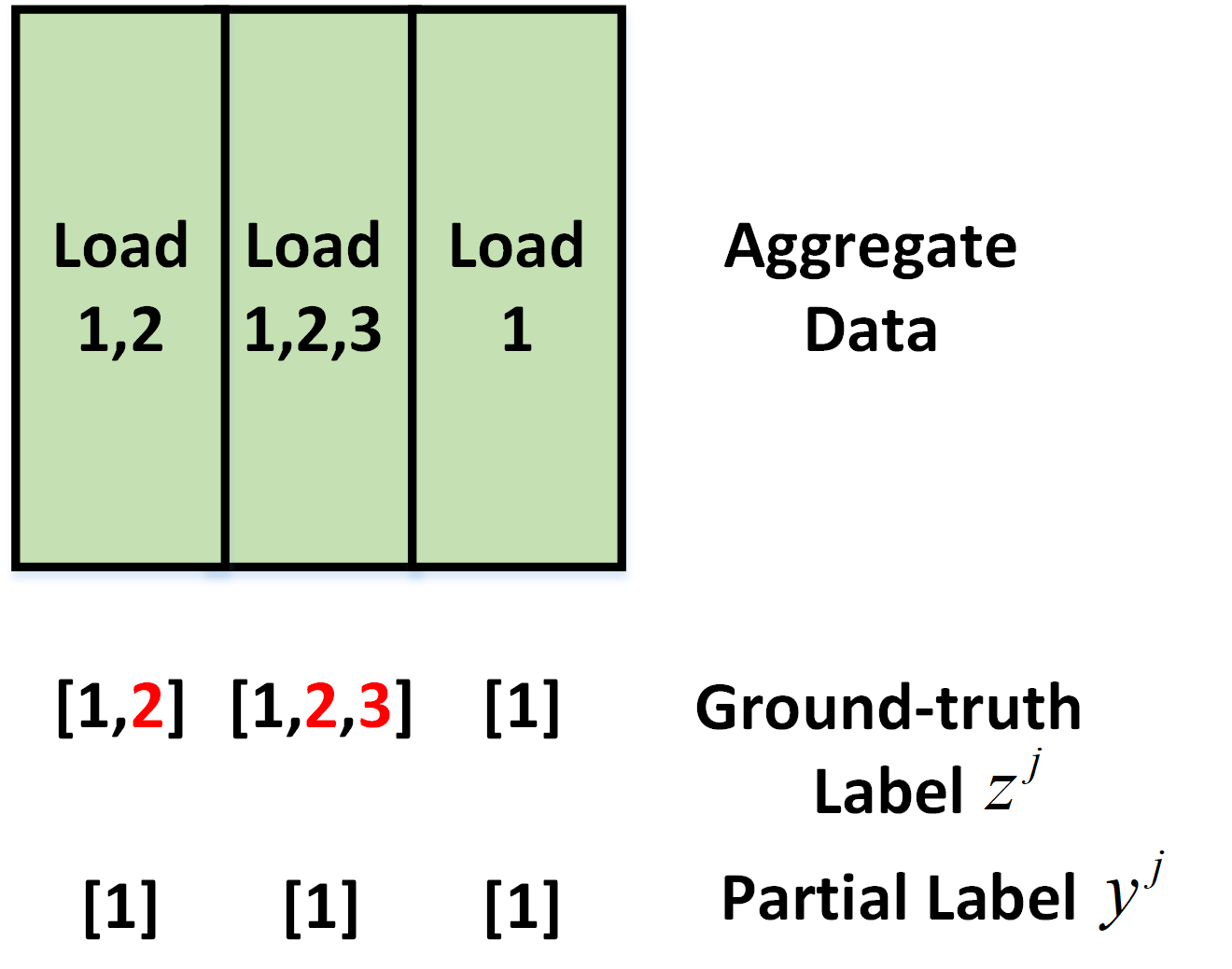
Energy disaggregation at the substation level (EDS) estimates the energy consumption of each type of load from the aggregated measurements. At the substation level, most meters only measure at the net point so the obtained measurements are aggregated loads. It may be difficult to identify a set of pure measurements of a certain type of load. The distribution operator may know all the loads connected to a substation, it may not know whether a particular type of load is consuming energy or not within a given time interval. Thus, each aggregate measurement is the total consumption of multiple types of loads, and the types that exist in this measurement are not fully known. We call it “partially labeled aggregate data.” We for the first time addresses the so-called “partial labels” issue in energy disaggregation and develops a model-free EDS method to separate individual loads, including BTM solar, from the total energy consumption in real-time.
Energy disaggregation at the substation level and illustration of partial labels
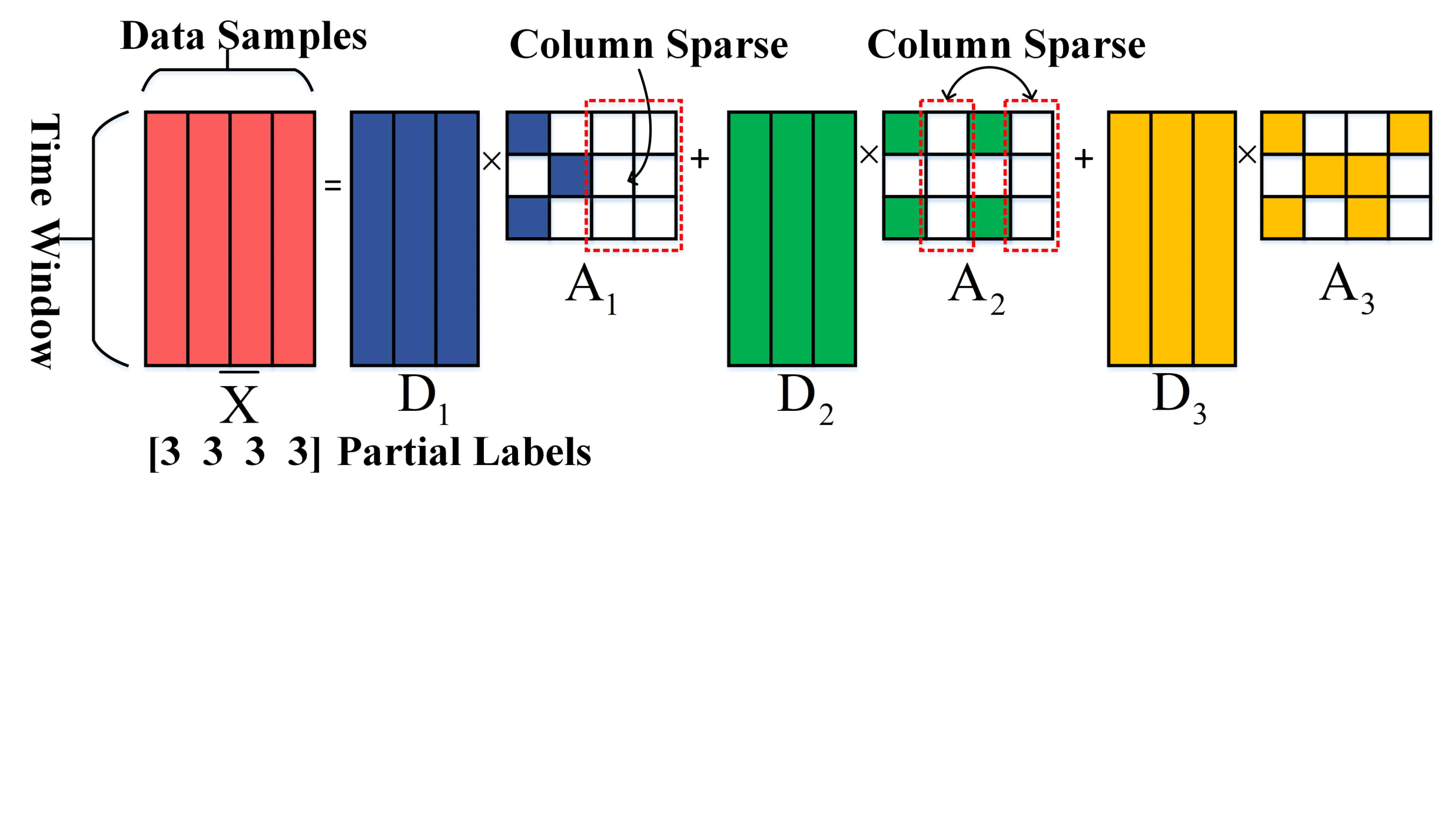
Proposed mathmatical model

Bayesian Energy Disaggregation at Substations with Uncertainty Modeling
The existing energy disaggregation method cannot provide any reliability measure of the disaggregation results, while the disaggregation accuracy can vary significantly for different data due to the volatility of loads such as the solar generation. We proposes a Bayesian-dictionary-learning-based approach to disaggregate the loads and provides an uncertainty measure of the returned estimation. Our approach learns the probability distributions of the load patterns and the decomposition coefficients from recorded data with partial labels at the offline stage. In real-time disaggregation of the obtained aggregate data, our approach computes the mean and covariance of the probability distribution of each load consumption, estimates the load using the mean, and computes the uncertainty index based on the covariance.
Diaggregation results of existing method (without the uncertainty measure):

.png)
.png)
.png)
Diaggregation results of proposed method (provide the uncertainty measure)

.png)
.png)
.png)
The framework of proposed graphic model

Bayesian Robust Hankel Matrix Completion with Uncertainty Modeling for Synchrophasor Data Recovery
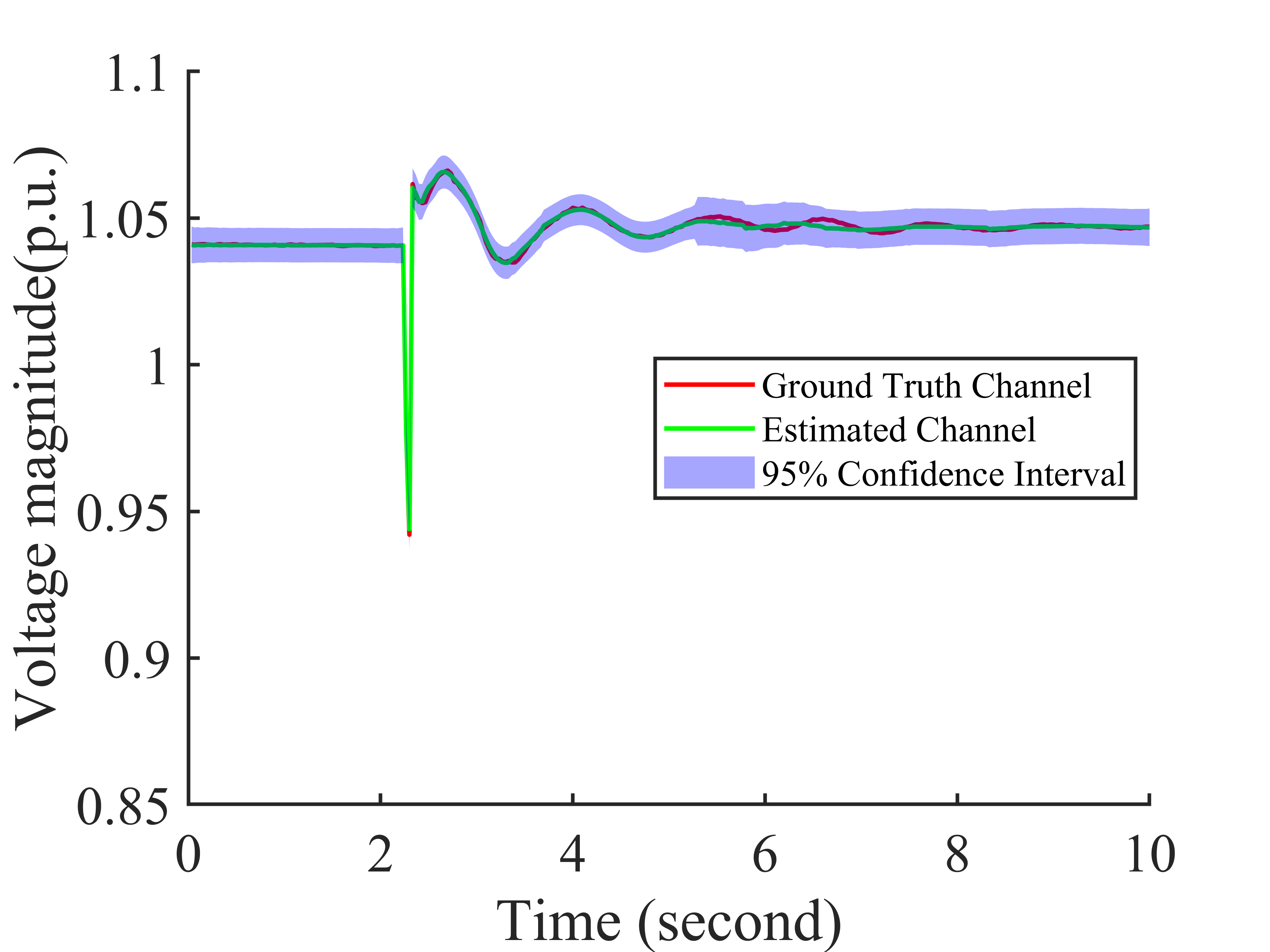
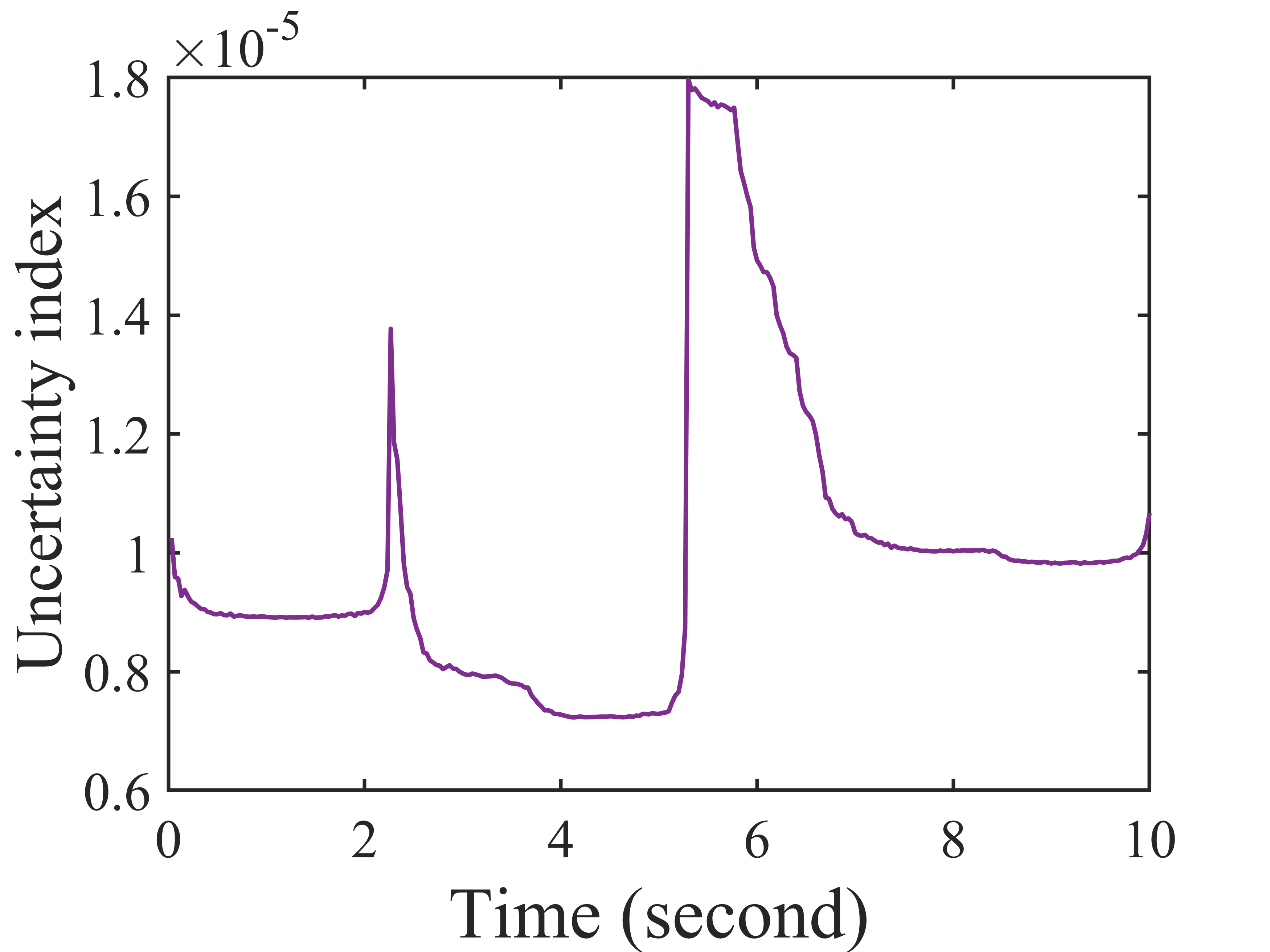
Synchrophasor data suffer from quality issues like missing and bad data. Exploiting the low-rankness of the Hankel matrix of the synchrophasor data, we formulate the data recovery problem as a robust low-rank Hankel matrix completion problem and proposes a Bayesian data recovery method that estimates the posterior distribution of synchrophasor data from partial observations. In contrast to the deterministic approaches, our proposed Bayesian method provides an uncertainty index to evaluate the confidence of each estimation. To the best of our knowledge, this is the first method that provides confidence measure for synchrophasor data recovery.
Recovery results of proposed method (provide the uncertainty measure)
Additional Gaussian noise is added during time 5.6 to 6.6 seconds. The subfigures are (a) the observed data, (b) the estimated data, (c) the estimated data in one channel (d) the uncertainty index for the channel in (c).
The framework of proposed graphic model
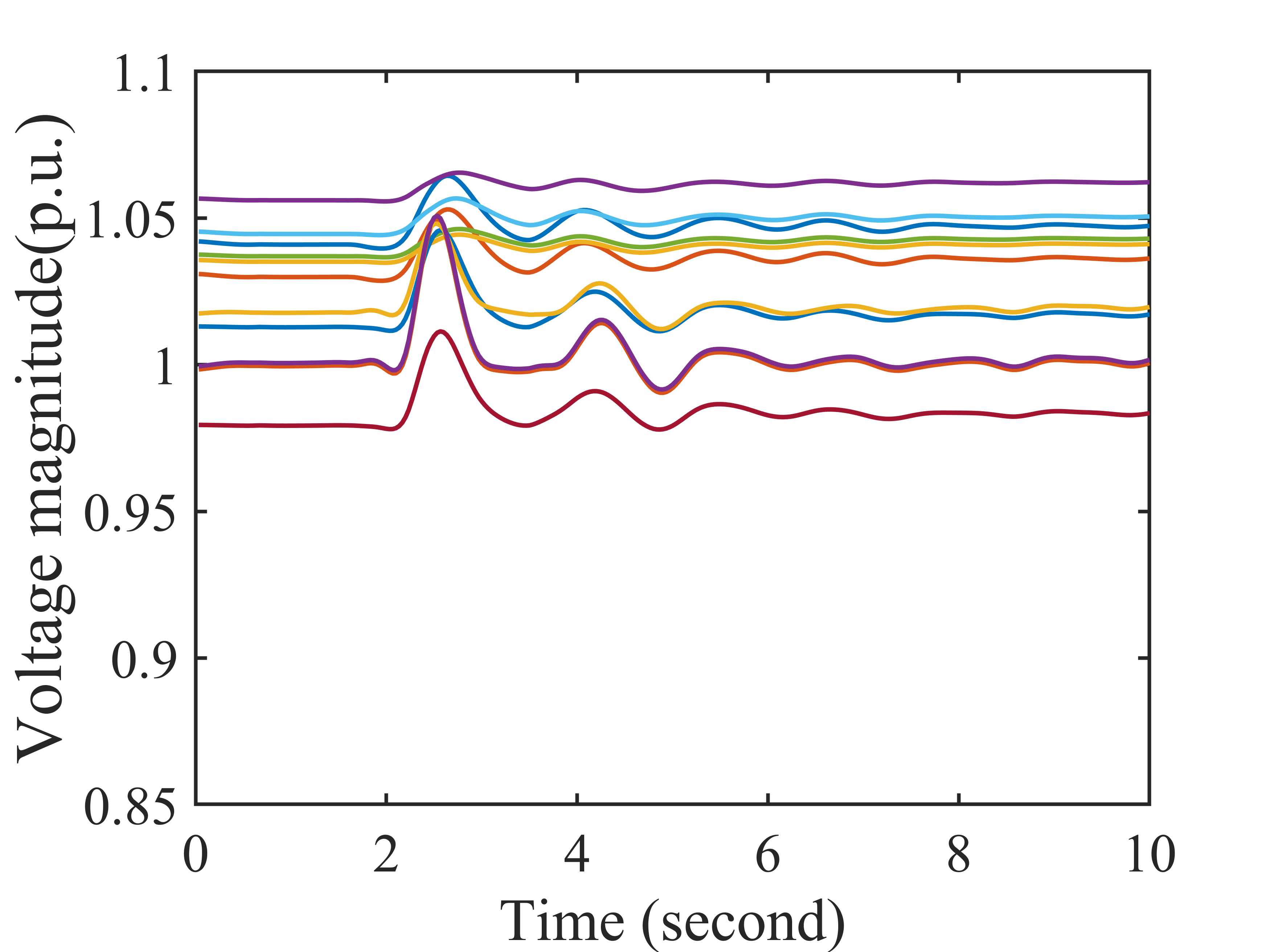
Bayesian High-Rank Hankel Matrix Completion for Synchrophasor Data Recovery
The existing works exploit the Hankel low-rankness of the PMU data. However,many PMU data do not satisfy the low-rank property because of the nonlinear dynamics. Applying the approximate low-rankness to the PMU data recovery sometimes leads to degradation of the recovery performance. We develop a new Bayesian method to implicitly map the high-rank nonlinear data into the high dimensional space by the kernel trick. We propose to exploit the lifted low-rankness of the Hankel matrix of the data in the high dimensional space, although the rank of the data in the original low dimensional space is high.
Comparison of recovery results of proposed high-rank method with two low-rank methods
The subfigures are (a) the observed data, (b) the estimated data by our method, (c) the estimated data by Bayesian low-rank method (d) the estimated data by deterministic low-rank method.



Streaming Synchrophasor Data Quality (SSDQ) Software for EPRI
I also mentor several undergraduate students to implement the our developed data recovery algorithms on Matlab and OpenPDC/OpenECA platform. OpenPDC is an open source platform for streaming synchrophasor data, used by ISO New England, the Tennessee Valley Authority (TVA), Southern Company, Southwest Power Pool (SPP).
Demo of developed software on OpenECA and Matlab GUI Platform
